In optical terms, the word "aperture" refers to a hole or an opening which light travels through.
In photography, the aperture simply refers to the diameter of the opening of a lens.
This table (from the first article in this series on understanding your camera) provides a summary of the effect of aperture:
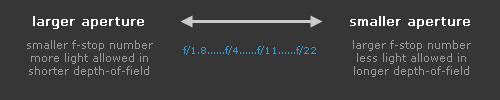
Adjusting the aperture of a lens adjusts the diameter of the hole in the lens, thus controlling the amount of light that reaches the camera's sensor (or film). Setting a smaller aperture results in this hole being smaller, and thus allows less light onto the camera's sensor.
In photography, a stop is a unit used to measure ratios of light or exposure. Adjusting the aperture by one stop adjusts the amount of light passing through by a factor of two.
In other words, changing to a smaller aperture by one stop will reduce the amount of light by half, which means the size of the hole (the area) is reduced by half.
The series of photos below show the size of the hole set by the aperture blades on a Canon EF 35mm f/2 lens, with the aperture decreasing a full stop between each image (the left image shows a large aperture, and moving to the right shows successively smaller aperture settings).

f/4
|

f/5.6
|

f/8
|

f/11
|
An aperture of f/4 allows twice as much light as f/5.6, and f/5.6 allows twice as much light as f/8, etc.
Note that a camera normally keeps the lens wide open at its maximum aperture most of the time, to provide a brighter image in the viewfinder. It only closes down the aperture to the required aperture setting when the camera is taking a photo.
Many cameras have a depth-of-field preview button, which, when depressed, will cause the camera to set the lens' aperture to the specified setting (resulting in a darker image in the viewfinder if a smaller aperture than lens' maximum is being used).
Warning: this section contains the mathematics behind aperture stops. If you are not interested in the mathematics, you can skip over this section, and read the next non-mathematics part of this article.
As mentioned earlier, each f-stop reduces the amount of light by a half, so it's reducing the area of the lens opening by half. This means it's reducing the diameter of the lens opening by a factor of the square root of 2.
Common f-stops are as follows (all spaced by a full stop):
f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, etc
The f-stop number can be calculated using the following:
Calculating out the first 10 f-stop numbers gives:
| f/1 | = f / (sqrt(2)^0) | = f/1 |
| f/1.4 | = f / (sqrt(2)^1) | = f/1.4142 |
| f/2 | = f / (sqrt(2)^2) | = f/2 |
| f/2.8 | = f / (sqrt(2)^3) | = f/2.8284 |
| f/4 | = f / (sqrt(2)^4) | = f/4 |
| f/5.6 | = f / (sqrt(2)^5) | = f/5.6569 |
| f/8 | = f / (sqrt(2)^6) | = f/8 |
| f/11 | = f / (sqrt(2)^7) | = f/11.3137 |
| f/16 | = f / (sqrt(2)^8) | = f/16 |
| f/22 | = f / (sqrt(2)^9) | = f/22.6274 |
Note that these numbers are rounded to make them easier to use.
With modern cameras, the aperture is controlled by the camera body, and not by a rotating ring on the lens itself. Because of this, with most modern cameras, you are not limited to full f-stops, but can use intermediate f-stops. Some cameras allow 1/2 f-stop increments, but most allow 1/3 f-stop increments.
Here is a sequence of 1/3 increment f-stops, with the increments matching a full f-stop in bold, and the 1/3 increments in normal text:
f/2.8, f/3.2, f/3.5, f/4, f/4.5, f/5, f/5.6, f/6.3, f/7.1, f/8, etc
The depth-of-field of a photo refers to how much of the subject material is in focus. With a short depth-of-field, only a small amount is in focus (ie, a portrait with the background completely blurred and out-of-focus), while with a larger depth-of-field, more of the foreground and background will be in focus.
Using a large aperture (ie, a small f-stop number, such as f/2.8) will result in a short (shallow) depth-of-field, while using a small aperture (such as f/22) will result in a much larger depth-of-field.
Here are a couple of photos demonstrating the effect of aperture on the depth-of-field. Both photos were taken from exactly the same location, but the first photo shows a very short depth-of-field due to the use of a large aperture, which causes the (distracting) background to be completely blurred.
The second photo shows a much larger depth-of-field due to a much smaller aperture.


Many people refer to "stopping down" a lens. To stop down a lens just means you are using a smaller aperture (ie, larger f-stop number), thus reducing the amount of light that can pass through the lens to the camera.
Similarly, opening up a lens refers to going to a larger aperture (ie, smaller f-stop number), thus letting more light through the lens and to the camera.
The maximum aperture of a lens is when the aperture diameter is the largest - that is, when the f-stop number has the smallest denominator.
Many consumer lenses typically have a maximum aperture of f/4, while faster lenses can have a maximum aperture of f/2.8, f/1.8 or larger.
Lenses with a larger maximum aperture are faster because their larger aperture allows more light to reach the camera sensor (or film), thus allowing shorter (faster) shutter speed in a given lighting situation.
For this reason, fast lenses are good for low-light photography, and are also useful for achieving a short depth-of-field, desirable in portrait photography, where the subject needs to be in focus, but the background suitably blurred.
Fast lenses require larger diameter optics, which typically results in lenses that are larger, heavier and more expensive than slower lenses. For example, if you compare the size of Canon's 50mm f/1.8, 50mm f/1.4 and 50mm f/1.2 lenses, the f/1.4 is larger, heavier and more expensive than the f/1.8, and similarly, the f/1.2 is the largest, heaviest and most expensive of the trio.
Some lenses have an aperture range, rather than specifying the maximum aperture as a single value. For example, Canon's EF-S 18-55mm IS lens has an aperture range of f/3.5 - 5.6.

Lenses with an aperture range do not have the same maximum aperture across their zoom range. In the case of the Canon EF-S 18-55mm IS lens, it means it has a maximum aperture of f/3.5 at the wide end (18mm), and a maximum aperture of f/5.6 when fully zoomed at 55mm.
This behaviour is largely driven by economics - ie, a lens with a constant maximum aperture is more expensive to make, such as the much-more-expensive Canon EF 24-70mm f/2.8L lens.




Very informative!